古法手搓三维模型数据，顶点 UV 索引概念一文搞定！（vertices uv indices）

时间：2025-8-4 14:13 作者：独元殇 分类： WebGL

[toc]

introduce

工具地址：https://git.ccgxk.com/vtool/vtool.html

今天要通过一个我精心制作的网页工具，手把手教大家手搓一个六棱柱。让大家（尤其是图形学初学者）一文搞懂抽象的顶点、UV、索引。我们可能经常见过这些数据，也经常用，但我们很有可能搞了半年三维了，却不一定真的知道它们怎么写、它们的具体概念。毕竟成熟的软件导出模型，直接会帮我们做好这些底层工作，我们完全无需了解......

↑ 手搓工具示意图

什么是三维模型顶点数据？

这是在图形学里面，组成一个三维模型的基本元素，包括每个顶点的坐标、每个面的法线、纹理坐标（UV）、颜色、面的索引等等，这里以 webgl 为例子，要想建立一个小模型，最基本的元素是 ----- 顶点坐标。

比如说你想搞一个立方体，那么最简单的方式就是把 8 个顶点坐标给确定了，然后按照一定的顺序来写就能让 webgl 画出来，嘿嘿。

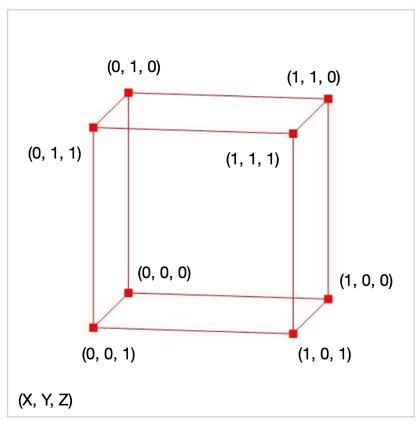
↑ 一个立方体的各个顶点的坐标

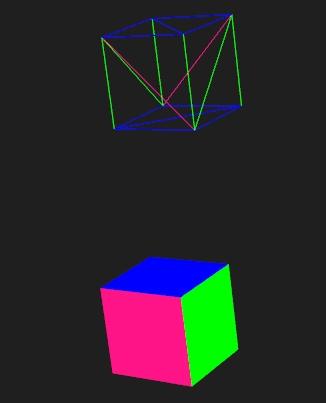
↑ 立方体每个面由三角组成的示意图

在三维模型里，面都是由三角形组成的，因为三角形能组合成任意的形状嘛 o(￣▽￣)ｄ，无论是矩形、六边形、还是五角星.....
在写顶点时，按照三角形的顺序，三三一组来写，就能写出一个立方体。
这是最古老的方法了。可是！只要我们一实践，马上就能发现一个问题！
我们原以为，不就 8 个点吗？等我们写出来，我们会发现在浏览器上一个一眼能望穿的立方体，竟然得写 8 × 2 = 16 个三角形组（），8 × 2 × 3 = 48 行，长长的数据（如代码所示）：

// 一个立方体的顶点数据
const vertices = new Float32Array([
    // === 1. 前面 (Front Face) ===
    // 第一个三角形
   -0.5, -0.5,  0.5,  // 左下角
    0.5, -0.5,  0.5,  // 右下角
    0.5,  0.5,  0.5,  // 右上角
    // 第二个三角形
   -0.5, -0.5,  0.5,  // 左下角 
    0.5,  0.5,  0.5,  // 右上角 
   -0.5,  0.5,  0.5,  // 左上角

    // === 2. 后面 (Back Face) ===
    // 第一个三角形
   -0.5, -0.5, -0.5,  // 左下角
    0.5,  0.5, -0.5,  // 右上角
    0.5, -0.5, -0.5,  // 右下角
    // 第二个三角形
   -0.5, -0.5, -0.5,  // 左下角
   -0.5,  0.5, -0.5,  // 左上角
    0.5,  0.5, -0.5,  // 右上角

    // === 3. 上面 (Top Face) ===
    // 第一个三角形
   -0.5,  0.5,  0.5,  // 前左上
    0.5,  0.5,  0.5,  // 前右上
    0.5,  0.5, -0.5,  // 后右上
    // 第二个三角形
   -0.5,  0.5,  0.5,  // 前左上
    0.5,  0.5, -0.5,  // 后右上
   -0.5,  0.5, -0.5,  // 后左上

    //=== 4. 下面 (Bottom Face) ===
    // 第一个三角形
   -0.5, -0.5,  0.5,  // 前左下
    0.5, -0.5, -0.5,  // 后右下
    0.5, -0.5,  0.5,  // 前右下
    // 第二个三角形
   -0.5, -0.5,  0.5,  // 前左下
   -0.5, -0.5, -0.5,  // 后左下
    0.5, -0.5, -0.5,  // 后右下

    // === 5. 右面 (Right Face) ===
    // 第一个三角形
    0.5, -0.5,  0.5,  // 前右下
    0.5, -0.5, -0.5,  // 后右下
    0.5,  0.5, -0.5,  // 后右上
    // 第二个三角形
    0.5, -0.5,  0.5,  // 前右下
    0.5,  0.5, -0.5,  // 后右上
    0.5,  0.5,  0.5,  // 前右上

    // === 6. 左面 (Left Face) ===
    // 第一个三角形
   -0.5, -0.5,  0.5,  // 前左下
   -0.5,  0.5,  0.5,  // 前左上
   -0.5,  0.5, -0.5,  // 后左上
    // 第二个三角形
   -0.5, -0.5,  0.5,  // 前左下
   -0.5,  0.5, -0.5,  // 后左上
   -0.5, -0.5, -0.5   // 后左下
  ]
]);

（注：这个数据，是以立方体中心为 0,0,0 的）
长度可能会惊掉我们的下巴，哈哈。现在，我们就来使用我们的工具来将其写到我们的页面上。以便后面的学习！

手搓工具的使用

在线地址在这里 ->：手搓模型顶点数据工具

当然，如果想下载的话，直接 Ctrl + S 保存网页也行，但很遗憾，因为跨域请求的原因，只有在 http 环境下才能加载图片纹理，这个要注意。

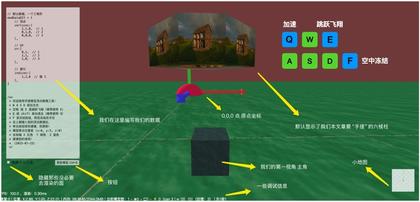
↑ 我的这个工具的界面介绍图

不同于三维设计软件热衷于的第三视角旋转平移缩放，俺这个工具是第一视角的，类似于 GTA 游戏、fps 游戏。但有稍稍不一样：

Q 是加速跑的（游戏里是 shift，容易手累）
E 可以代替空格，然后跑步（空格键声音太大了，被人骂过 o(╥﹏╥)o），另外，跳跃可以接连跳，类似于飞翔！
F 是空中冻结。因为内置了一个迷你版的 29kb 的 cannon 物理引擎，它跳到了空中会因重力下落，单击 F 键，可以暂时冻在空中！然后供我们环绕！

而左侧是编辑框，也使用了大名鼎鼎的 areaEditor.js ，一个只有 2kb 的超轻量级代码编辑器，能自动换行、括号补全、tab 补全......
打开后，编辑框里面默认显示了我们本节的最终结果，一个简简单单，矮矮的六棱柱！现在，我们先将上一节的立方体数据输入进来，体会一下它的使用！

使用数据生成一个立方体

第一步，删去里面的杂项，只留下下面的内容（也就是我们现在只需要顶点）：

modDataDIY = {
    // 顶点
    vertices:[],
}

第二步，我们使用伟大的复制粘贴，将关键的代码，也就是我们的立方体顶点数据粘贴进去，最终如下：

modDataDIY = {
    // 顶点
    vertices:[
        -0.5, -0.5,  0.5,  
        0.5, -0.5,  0.5,  
        0.5,  0.5,  0.5,  
        -0.5, -0.5,  0.5,   
        0.5,  0.5,  0.5,   
        -0.5,  0.5,  0.5,  

        -0.5, -0.5, -0.5,  
        0.5,  0.5, -0.5,  
        0.5, -0.5, -0.5,  
        -0.5, -0.5, -0.5,  
        -0.5,  0.5, -0.5,  
        0.5,  0.5, -0.5,  

        -0.5,  0.5,  0.5,  
        0.5,  0.5,  0.5,  
        0.5,  0.5, -0.5,  
        -0.5,  0.5,  0.5,  
        0.5,  0.5, -0.5,  
        -0.5,  0.5, -0.5,  

        -0.5, -0.5,  0.5,  
        0.5, -0.5, -0.5,  
        0.5, -0.5,  0.5,  
        -0.5, -0.5,  0.5,  
        -0.5, -0.5, -0.5,  
        0.5, -0.5, -0.5,  

        0.5, -0.5,  0.5,  
        0.5, -0.5, -0.5,  
        0.5,  0.5, -0.5,  
        0.5, -0.5,  0.5,  
        0.5,  0.5, -0.5,  
        0.5,  0.5,  0.5,  

        -0.5, -0.5,  0.5,  
        -0.5,  0.5,  0.5,  
        -0.5,  0.5, -0.5,  
        -0.5, -0.5,  0.5,  
        -0.5,  0.5, -0.5,  
        -0.5, -0.5, -0.5   
  ],
}

然后，单击更新模型按钮，然后我们画面里就出现了一个立方体！！！

↑ 生成的立方体

我们可以四处转转，观摩一下我们的这个立方体。现在我们基本会用这个工具了，接下来正式进入教学。

画三角

现在，我们刷新页面，单击更新模型，模型会变成默认的三角形。
好，我们先从最简单的一个三角形的面开始：

modDataDIY = {
    // 顶点
    vertices:[
        1,1,0,  // 0
        0,1,0,  // 1
        0,0,0,  // 2
    ],

    // UV
    uv:[
        0,1,  // 0
        1,1,  // 1
        1,0,  // 2
    ],

    // 索引
    indices:[
        1,2,0  // 面 1
    ],
}

效果是这样：

↑ 最最最简单的三角形！

现在，我们就来讲一下，这三块数据分别代表什么！

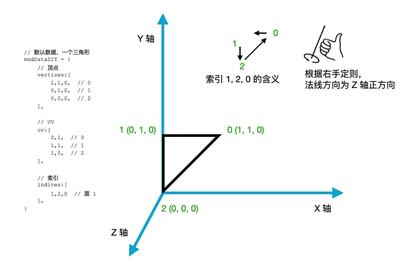
↑ 顶点和索引

首先是顶点和索引。
顶点，在上一个章节里，我们有了解。在这个三角形中，顶点如上图所示。

每三个为一组，三行顶点，分别对应 0 点、1 点、2 点。系统会自动给我们分好类，这个就是点的编号！

这个编号，我们可以用在索引里！

那么这个三角形的索引，1, 2, 0 就可以表示我们的三角形了！我们就不用重复写点了！

问题来了，索引表示点的顺序是怎么样的？ 1,2,0 1,0,2 等等有区别吗？当然有区别了！

在 Webgl 里，每个面都有一个法线方向，用于确定哪边是面的正面，哪边是面的背面！这个时候就用到右手定则了。四个卷手指指向我们的索引顺序方向，此时大拇指指向的就是我们的面的法向法向了！

1, 2, 0 是逆时针，法向方向是 Z 轴正方向。

1, 0, 2 是顺时针，法线方向是 Z 轴负方向。

可是法向方向，也就是面的正面，定义这个有什么用？

它的用途很多，但最有标志性的就是面剔除！

面剔除

在我们的工具左下角，有一个「隐藏不可见面」的勾选框，我们现在操作画面，绕到三角形前后面看一下，之后勾选后再看一下。

↑ 背面看不到三角形了

我们会发现勾选后，这个三角形只有正面会显示，而背面不显示。
这就是法线的最大意义，它规定了正面后，我们可以将另一个面剔除。
这样做有什么意义呢？
首先，什么叫「不可见面」！在这个赤裸裸的三角形里我们当然感觉没有用，但是在一些封闭的三维体呢？比如刚才的立方体，在正常情况下，我们肯定是不会看到立方体里面那个面的，因此，我们如果将每个面的法向都朝向外面，然后使用这个「面剔除」工具，这样我们的电脑就不会再去渲染立方体内部了，渲染压力顷刻间减少一半，意义非凡 (〃'▽'〃) ！！！

传说中的 UV 是什么？

现在我们明白顶点、索引、法向了吧！！
接下来就是 UV 了。
UV 数据，三行分别对应三个点。我们为三个点，分别分配一个图的坐标，之后引擎会自动对这个图进行拉伸翻转，以适应我们的坐标。

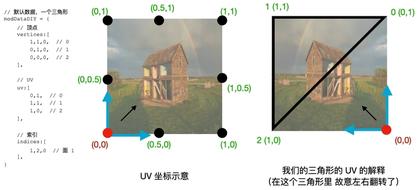
↑ UV 坐标的解析

在我们的引擎里，每张图的左下为 (0, 0)，右上为 (1, 1)，如上图的左边的图为例（不同的渲染引擎，可能略有不同，以那些引擎的文档说明为最终依据）。
而如果我们将左下角的点定义成 (1, 0) 而不是 (0 ,0)、且左上角定义成 (1, 0) 或右上定义成 (0, 1)，那就会左右翻转....... 当然，你也可以想象一下怎么样就会上下翻转...
在我们的例子里，我们为这三个点分别分配那三个坐标，最终图片可不就是左右翻转...... （0, 0）到最右下了。
现在我们的纹理是左右翻转的，如果我们将 uv 改为如下，则图片将正常显示（大家仔细琢磨一下，该怎么改呢？？没错，就是 2 点对应（0, 0））：

    // UV
    uv:[
        1,1,  // 0
        0,1,  // 1
        0,0,  // 2
    ],

那么结果就是正常显示了！

↑ 图片正常显示

如果我们以下面这种写法来写，那就上下颠倒了！

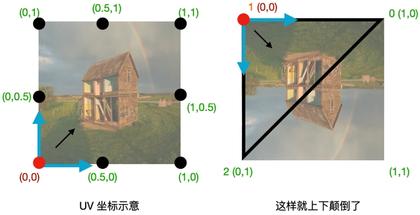
↑ 上下颠倒就是 0(1,0) 1(0,0) 2(0,1)

那么代码就是：

    // UV
    uv:[
        1,0,  // 0
        0,0,  // 1
        0,1,  // 2
    ],

单击更新模型，效果是这样：

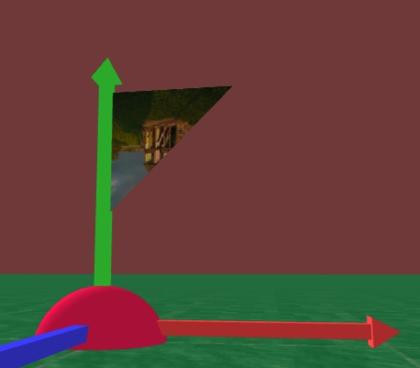
↑ 结果显然，上下颠倒了

那么如果不写 1 和 0 ，我们写成 (0.5, 0) 或 (5, 5) 这种呢？

↑ 两种奇葩写法的示意图

我们可以自己修改代码，它们最终的显示效果会分别如下所示：

↑ (5, 5) 写法

↑ (0.5, 0.5) 写法

当然，如果你使用不老实的写法，比如 (3.14 , 0) .....，那么它也会老老实实的扭曲一下。大家感兴趣可以试试......

搞一个正方形

基础知识我们掌握完毕，现在开始出活儿！

我们绘制了一个三角形了，我们现在需要将其补全，绘制为一个平面！

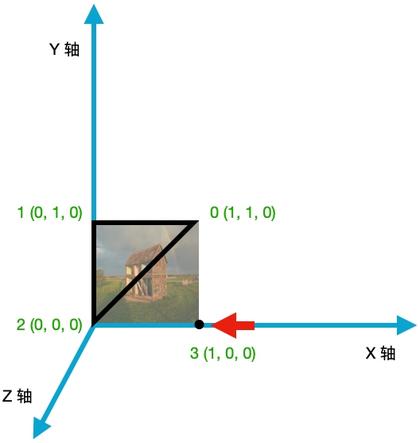
↑ 第 4 个点，即点三的示意图

我们现在添加第四个点，即点 3 (1, 0, 0)。

显然，它的 UV 应该是 (1,0)

显然，这是第二个面，所以索引要新增加一个 0, 2, 3 。

我们把代码整理一下，如下所示：

modDataDIY = {
    // 顶点
    vertices:[
        1,1,0,  // 0
        0,1,0,  // 1
        0,0,0,  // 2
        1,0,0,  // 3 <-
    ],

    // UV
    uv:[
        1,1,  // 0
        0,1,  // 1
        0,0,  // 2
        1,0,  // 3 <-
    ],

    // 索引
    indices:[
        1,2,0, // 面 1
        0,2,3, // 面 2 <-
    ],
}

最终的结果，也很如人意！

↑ 一个正方形

之后，就是我们的「六棱柱」策划了！

策划六棱柱

首先说明一下，我们以学习为主，所以搞的不是正六棱柱，那个还得计算 π，太麻烦。我们就以最简单的 0 1 2 来定义坐标。

因为点并不多，所以我们在纸上将所有点先都画出来，算好我们的坐标，12 个点每个点的坐标。

我们三棱柱每个点的坐标

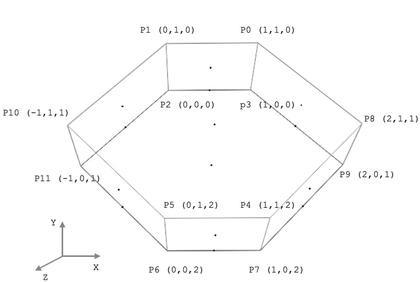
↑ 我们先做第二个面吧，即 P4 P5 P6 P7 那个面。

按照我们做的第一个正方形的样子，做第二个正方形，代码如下：

modDataDIY = {
    // 顶点
    vertices:[
        1,1,0,  // 0
        0,1,0,  // 1
        0,0,0,  // 2
        1,0,0,  // 3

        1,1,2,  // 4
        0,1,2,  // 5
        0,0,2,  // 6
        1,0,2,  // 7
    ],

    // UV
    uv:[
        1,1,  // 0
        0,1,  // 1
        0,0,  // 2
        1,0,  // 3

        1,1,  // 4
        0,1,  // 5
        0,0,  // 6
        1,0,  // 7
    ],

    // 索引
    indices:[
        // 后面
        1,2,0, // 三角形 1
        0,2,3, // 三角形 2

        // 前面
        4,5,6,  // 三角形 1
        4,6,7,  // 三角形 2
    ],
}

效果如下，还可以：

↑ 第二个面搞好了

然后做右前那个面。（P8 P4 P7 P9 那个面）

此时。我们会遇到一个问题.... UV 怎么写？？？

点重复了，我们的「前面」的 P4 使用 UV 一次，我们的「右前」又要使用一次 UV.....

是的，很遗憾， UV 并不会看索引，UV 只会根据点，所以我们还要再写一次顶点。唉.... 即便使用了索引，还是顶点重复。

现在，我们的代码如下：

modDataDIY = {
    // 顶点
    vertices:[
        1,1,0,  // 0
        0,1,0,  // 1
        0,0,0,  // 2
        1,0,0,  // 3

        1,1,2,  // 4
        0,1,2,  // 5
        0,0,2,  // 6
        1,0,2,  // 7

        2,1,1,  // 8
        1,1,2,  // 9 (4)
        1,0,2,  // 10 (7)
        2,0,1,  // 11 (9)
    ],

    // UV
    uv:[
        1,1,  // 0
        0,1,  // 1
        0,0,  // 2
        1,0,  // 3

        1,1,  // 4
        0,1,  // 5
        0,0,  // 6
        1,0,  // 7

        1,1,  // 8
        0,1,  // 9
        0,0,  // 10
        1,0,  // 11

    ],

    // 索引
    indices:[
        // 后面
        1,2,0, // 三角形 1
        0,2,3, // 三角形 2

        // 前面
        4,5,6,
        4,6,7,

        // 右前
        8,9,10,
        8,10,11,
    ],
}

效果还可以：

↑ 「右前」面搞好了

但我们不想这样重复眼花缭乱的定义坐标，那么我们就来搞个 js 吧。
我们事先，将这 12 个点定义好。如下所示：

var p0 = [1,1,0];
var p1 = [0,1,0];
var p2 = [0,0,0];
var p3 = [1,0,0];
var p4 = [1,1,2];
var p5 = [0,1,2];
var p6 = [0,0,2];
var p7 = [1,0,2];
var p8 = [2,1,1];
var p9 = [2,0,1];
var p10 = [-1,1,1];
var p11 = [-1,0,1];

接着使用 Array.fill() 结合展开语法 ... 将其嵌入到我们的顶点数组里，也就是类似下面这种语法：

var test = [1,2,3,4];
var myArr = [0,0,0,...test,0,0,0]
// 等同于 myArr = [0, 0, 0, 1, 2, 3, 4, 0, 0, 0]

那么就会大大的提高我们的手搓效率！
当然，UV 的模式也是一直在重复使用的，也可以抽离出来，于是我们可以这样写！一口气就能把我们的 6 个面都搞完！

var p0 = [1,1,0];
var p1 = [0,1,0];
var p2 = [0,0,0];
var p3 = [1,0,0];
var p4 = [1,1,2];
var p5 = [0,1,2];
var p6 = [0,0,2];
var p7 = [1,0,2];
var p8 = [2,1,1];
var p9 = [2,0,1];
var p10 = [-1,1,1];
var p11 = [-1,0,1];
var uvDefault = [1,1,0,1,0,0,1,0]; // 默认uv

modDataDIY = {
    // 顶点
    vertices:[
        ...p0,...p1,...p2,...p3, //后
        ...p4,...p5,...p6,...p7, //前
        ...p8,...p4,...p7,...p9, //右前
        ...p0,...p8,...p9,...p3, //右后
        ...p5,...p10,...p11,...p6,//左前
        ...p10,...p1,...p2,...p11,//左后
    ],

    // UV
    uv:[
        ...uvDefault,...uvDefault, //后前
        ...uvDefault,...uvDefault, //右前后
        ...uvDefault,...uvDefault, //左前后
    ],

    // 索引
    indices:[
        //1,2,0,0,2,3,// 后面(错误索引，删去)
        1,0,3,1,3,2,// 后面
        4,5,6,4,6,7,// 前面
        8,9,10,8,10,11,// 右前
        12,13,14,12,14,15,// 右后
        16,17,18,16,18,19,// 左前
        20,21,22,20,22,23,// 左后
    ],
}

看一下效果：

6 个面整整齐齐，看起来还不错！

貌似还不错，但是如果我们开始面剔除，也就是打钩隐藏不可见面的话..... 我们只希望朝外的面会被显示，很显然，我们的「后面」这个面，索引写错了。

1,0,3,1,3,2,// 「后面」索引修复！

这样，就正常了！

上下两个面之顶面

我们先搞「上面」。这是上面的点位图。我们这样规划三角形。当然，如果需要严谨的态度的话，这样显然是不行的，但我们只是学习，图省事！

「上面」的点位图：

按照法线朝外的顺序，很轻松就能写出来顶点和索引。

但是 UV 呢？这个时候，为了尽可能显示全图，图片可能会扭曲，但其实也不会太干扰观感。下面是每个点的 UV 值：

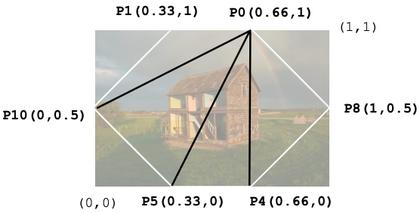
↑ 每个点的 UV 值

之后，我们很轻松就能将其写出来代码了！

var p0 = [1,1,0];
var p1 = [0,1,0];
var p2 = [0,0,0];
var p3 = [1,0,0];
var p4 = [1,1,2];
var p5 = [0,1,2];
var p6 = [0,0,2];
var p7 = [1,0,2];
var p8 = [2,1,1];
var p9 = [2,0,1];
var p10 = [-1,1,1];
var p11 = [-1,0,1];
var uvDefault = [1,1,0,1,0,0,1,0]; // 默认uv

modDataDIY = {
    // 顶点
    vertices:[
        ...p0,...p1,...p2,...p3, //后
        ...p4,...p5,...p6,...p7, //前
        ...p8,...p4,...p7,...p9, //右前
        ...p0,...p8,...p9,...p3, //右后
        ...p5,...p10,...p11,...p6,//左前
        ...p10,...p1,...p2,...p11,//左后

        //顶面 24~29
        ...p0,...p1,...p10,...p5,...p4,...p8,

    ],

    // UV
    uv:[
        ...uvDefault,...uvDefault, //后前
        ...uvDefault,...uvDefault, //右前后
        ...uvDefault,...uvDefault, //左前后
        // 顶面
        0.66,1,    0.33,1,
        0,0.5,    0.33,0,
        0.66,0,    1,0.5,
    ],

    // 索引
    indices:[
        //1,2,0,0,2,3,// 后面(错误索引，删去)
        1,0,3,1,3,2,// 后面
        4,5,6,4,6,7,// 前面
        8,9,10,8,10,11,// 右前
        12,13,14,12,14,15,// 右后
        16,17,18,16,18,19,// 左前
        20,21,22,20,22,23,// 左后
        24,25,26,   24,26,27,
        24,27,28,   24,28,29,
    ],
}

↑ 效果还可以

上下两个面之底面

然后就是最后一步了！

下面「底面」的坐标图：

↑ 「底面」的法向顺序

当然，要注意，我们是从下向上看，因此它的 UV 示意图是这样：

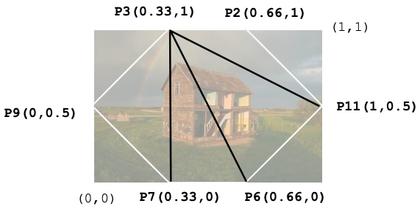
↑ 底面的 UV 示意图

现在我们应该很熟悉敲这个多边体的代码了。最终代码如下：

var p0 = [1,1,0];
var p1 = [0,1,0];
var p2 = [0,0,0];
var p3 = [1,0,0];
var p4 = [1,1,2];
var p5 = [0,1,2];
var p6 = [0,0,2];
var p7 = [1,0,2];
var p8 = [2,1,1];
var p9 = [2,0,1];
var p10 = [-1,1,1];
var p11 = [-1,0,1];
var uvDefault = [1,1,0,1,0,0,1,0]; // 默认uv

modDataDIY = {
    // 顶点
    vertices:[
        ...p0,...p1,...p2,...p3, //后
        ...p4,...p5,...p6,...p7, //前
        ...p8,...p4,...p7,...p9, //右前
        ...p0,...p8,...p9,...p3, //右后
        ...p5,...p10,...p11,...p6,//左前
        ...p10,...p1,...p2,...p11,//左后

        //顶面 24~29
        ...p0,...p1,...p10,...p5,...p4,...p8,
        //底面 30~35
        ...p2,...p3,...p9,...p7,...p6,...p11,
    ],

    // UV
    uv:[
        ...uvDefault,...uvDefault, //后前
        ...uvDefault,...uvDefault, //右前后
        ...uvDefault,...uvDefault, //左前后
        // 顶面
        0.66,1,    0.33,1,
        0,0.5,    0.33,0,
        0.66,0,    1,0.5,

        // 底面
        0.66,1,    0.33,1,
        0,0.5,    0.33,0,
        0.66,0,    1,0.5,
    ],

    // 索引
    indices:[
        //1,2,0,0,2,3,// 后面(错误索引，删去)
        1,0,3,1,3,2,// 后面
        4,5,6,4,6,7,// 前面
        8,9,10,8,10,11,// 右前
        12,13,14,12,14,15,// 右后
        16,17,18,16,18,19,// 左前
        20,21,22,20,22,23,// 左后
        // 顶面
        24,25,26,   24,26,27,
        24,27,28,   24,28,29,

        // 底面
        30,31,32,    30,32,33,
        30,33,34,    30,34,35,
    ],
}

最终，显示效果如下：